
Zadanie Muszkieterowie (mus)
Pomóż nam usprawnić bazę zadań!
Muszkieterowie
Limit pamięci: 32 MB
W czasach Ludwika XIII i jego potężnego ministra, kardynała Richelieu, w gospodzie pod Pełnym Antałkiem raczyło się jadłem i winem  muszkieterów. Wina było pod dostatkiem, a że muszkieterowie byli skorzy do zwady, doszło do wielkiej awantury, w której każdy muszkieter obraził wszystkich pozostałych.
muszkieterów. Wina było pod dostatkiem, a że muszkieterowie byli skorzy do zwady, doszło do wielkiej awantury, w której każdy muszkieter obraził wszystkich pozostałych.
Musiało dojść do pojedynków, ale kto miał się z kim pojedynkować i w jakiej kolejności? Uzgodnili (po raz pierwszy od awantury zrobili coś zgodnie), że staną na okręgu w ustalonej kolejności i będą ciągnąć losy. Wylosowany muszkieter toczył pojedynek ze swoim sąsiadem z prawej. Przegrany "odpadał z gry", a dokładniej - służący wynosili jego zwłoki. Sąsiadem wygrywającego stawał się następny muszkieter, stojący za przegranym.
Po latach, gdy historycy czytali wspomnienia zwycięzcy, spostrzegli, że ostateczny wynik zależał w istotny sposób od kolejności wylosowanych pojedynków. Zauważyli bowiem, że dotychczasowe treningi fechtunku pokazywały, kto z kim mógł wygrać pojedynek. Okazało się, że - mówiąc językiem matematycznym - relacja "A wygrywa z B" nie była przechodnia! Mogło się zdarzyć, że muszkieter A walczył lepiej od muszkietera B, B lepiej od C, a C lepiej od A. Oczywiście wśród takiej trójki wybór pierwszego pojedynku decydował o ostatecznym wyniku! Jeśli pierwsi będą walczyć A i B, to ostatecznie wygra C, ale jeśli pierwszymi będą B i C, to ostatecznie wygra A. Historycy, zafascynowani tym odkryciem, postanowili sprawdzić, którzy muszkieterowie mogli przeżyć - od tego zależał przecież los Francji, a wraz z jej losem, los całej cywilizowanej Europy!
Zadanie
Na okręgu stoi  osób, ponumerowanych kolejno liczbami od
osób, ponumerowanych kolejno liczbami od 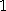 do
do  . Osoby te toczą
. Osoby te toczą 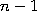 pojedynków. W pierwszej rundzie jedna z tych osób powiedzmy o numerze
pojedynków. W pierwszej rundzie jedna z tych osób powiedzmy o numerze 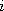 - toczy pojedynek z sąsiadem z prawej, tzn. osobą o numerze
- toczy pojedynek z sąsiadem z prawej, tzn. osobą o numerze 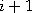 (lub, jeśli
(lub, jeśli 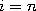 , to z osobą o numerze
, to z osobą o numerze 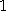 ). Przegrany odpada z gry, sąsiadem zwycięzcy staje się następna w kolejności osoba. Dana jest też tabela możliwych wyników pojedynków w postaci macierzy
). Przegrany odpada z gry, sąsiadem zwycięzcy staje się następna w kolejności osoba. Dana jest też tabela możliwych wyników pojedynków w postaci macierzy 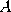 . Jeśli
. Jeśli  , to osoba o numerze
, to osoba o numerze 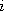 zawsze wygrywa z osobą o numerze
zawsze wygrywa z osobą o numerze 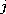 . Jeżeli
. Jeżeli  , to osoba o numerze
, to osoba o numerze 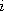 przegrywa z osobą o numerze
przegrywa z osobą o numerze 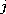 . Mówimy, że osoba
. Mówimy, że osoba  może wygrać zawody, jeżeli istnieje taki ciąg
może wygrać zawody, jeżeli istnieje taki ciąg 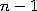 losowań, w wyniku którego będzie ona zwycięzcą ostatniego pojedynku.
losowań, w wyniku którego będzie ona zwycięzcą ostatniego pojedynku.
Napisz program, który:
- wczyta ze standardowego wejścia macierz
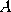 ,
, - wyznaczy numery osób, które mogą wygrać zawody,
- wypisze je na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia dana jest liczba całkowita  spełniająca nierówność
spełniająca nierówność 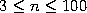 . W każdym z następnych
. W każdym z następnych  wierszy znajduje się jedno słowo złożone z
wierszy znajduje się jedno słowo złożone z  znaków 0 lub 1. Znak stojący na
znaków 0 lub 1. Znak stojący na 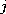 -tym miejscu w
-tym miejscu w 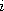 -tym z tych wierszy oznacza wartość
-tym z tych wierszy oznacza wartość 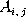 (tzn. jeśli tym znakiem jest jedynka, to
(tzn. jeśli tym znakiem jest jedynka, to 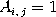 , a jeśli zero, to
, a jeśli zero, to 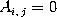 ). Oczywiście
). Oczywiście  , dla
, dla 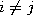 . Przyjmujemy, że
. Przyjmujemy, że  , dla każdego
, dla każdego 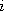 .
.
Wyjście
W pierwszym wierszu standardowego wyjścia należy zapisać liczbę 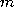 tych osób, które mogą wygrać zawody. W następnych
tych osób, które mogą wygrać zawody. W następnych 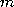 wierszach należy zapisać numery tych osób w kolejności rosnącej, po jednym numerze w wierszu.
wierszach należy zapisać numery tych osób w kolejności rosnącej, po jednym numerze w wierszu.
Przykład
Dla danych wejściowych:
7 1111101 0101100 0111111 0001101 0000101 1101111 0100001
poprawną odpowiedzią jest:
3 1 3 6
Kolejność pojedynków: 1-2, 1-3, 5-6, 7-1, 4-6, 6-1 daje ostateczną wygraną osobie o numerze 6. Można też sprawdzić, że jeszcze tylko osoby o numerach 1 i 3 mogą wygrać zawody.
Autor zadania: Wojciech Guzicki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English